[CASSANDRA-6474] Compaction strategy based on MinHash

• Type: New Feature
• Status: Open
• Priority: Normal
• Resolution: Unresolved
• Fix Version/s: 5.x
• Component/s: Local/Compaction
• Labels: compaction
• Assignee: Sankalp Kohli
• Reporter: Yuki Morishita

Authors

Sankalp Kohli

• Created: 11/Dec/13 05:40
• Updated: 23/Apr/23 20:36

Description

We can consider an SSTable as a set of partition keys, and 'compaction' as de-duplication of those partition keys.
We want to find compaction candidates from SSTables that have as many same keys as possible. If we can group similar SSTables based on some measurement, we can achieve more efficient compaction.
One such measurement is Jaccard Distance,

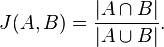
which we can estimate using technique called MinHash.

In Cassandra, we can calculate and store MinHash signature when writing SSTable. New compaction strategy uses the signature to find the group of similar SSTable for compaction candidates. We can always fall back to STCS when such candidates are not exists.

This is just an idea floating around my head, but before I forget, I dump it here. For introduction to this technique, Chapter 3 of 'Mining of Massive Datasets' is a good start.

Issue Links

• relates to: CASSANDRA-6216 Level Compaction should persist last compacted key per level